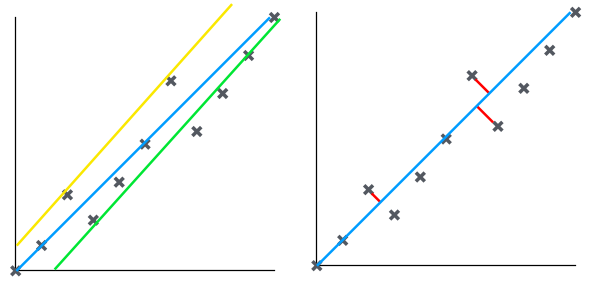
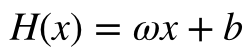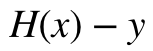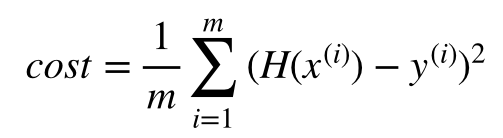전자세금계산서 엑셀 양식 작성 프로그램
ERP 시스템(전사적 자원 관리 시스템)을 통해 다운로드한 엑셀 파일을 가지고 전자세금계산서 발급을 위한 엑셀 양식 파일을 채우는 프로그램을 만들기로 했다. 기존에 사람이 직접 전자세금계산서 발급을 위해서 엑셀 양식을 채우는 과정에서 빈번한 실수가 발생하여 이를 방지하기 위해 프로그램을 개발할 필요성이 있었다.
따라서, 기존에 회사에서 발급 양식을 채우던 방식 그대로 꼭 필수 항목이 아니더라도 양식을 채우기로 했다.
고려사항
- 내가 받은 ERP 시스템에서 다운로드한 엑셀 파일에는 이메일 주소가 나와있지 않음
- 최대 1000건의 엑셀 데이터를 다루어야함
- 프로그래밍을 할 줄 모르는 사용자 고려 (프로그램을 실행하는 과정을 최대한 단순하게)
- openpyxl 라이브러리는 xls 확장자를 지원하지 않음
- 전자세금계산서 발급 양식은 어떤 경우에도 변경하지 않음
해결방안
- 별도의 이메일 주소가 담긴 엑셀 파일을 준비
- 파이썬의 openpyxl 라이브러리 사용
- 쉽게 프로그램을 사용할 수 있도록 별도의 웹서버 운영 (진행 중)
- ERP 시스템으로 xlsx 파일을 받을 수 있는지 확인, xlsx 파일로 전자세금계산서 발행이 가능한지 확인 (진행 중)
- 전자세금계산서 발급 양식은 불변하므로 별도의 머릿글 행(열 이름)을 처리하지 않음
사용 언어
- Python
데이터
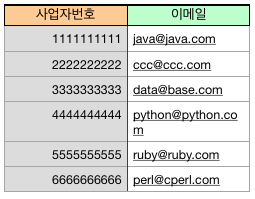
프로그램 테스트를 위해 사용한 데이터는 다음과 같다.
origin.xlsx
0.08MB
email.xlsx
0.01MB
erp.xlsx
0.03MB
코드
#!/usr/bin/env python
# coding: utf-8
import openpyxl
import os
import datetime
erpWB = openpyxl.load_workbook('data/erp.xlsx')
emailWB = openpyxl.load_workbook('data/email.xlsx')
taxWB = openpyxl.load_workbook('data/origin.xlsx')
erpWS = erpWB[erpWB.sheetnames[0]]
emailWS = emailWB.active
taxWS = taxWB[taxWB.sheetnames[0]]
# 이메일 사업자 번호를 키로 해쉬테이블
emailAddress = dict()
for i in range(2,emailWS.max_row+1):
emailAddress[emailWS[i][0].value] = emailWS[i][1].value
print(emailWS[i][0].value,emailAddress[emailWS[i][0].value])
# erp 수금 기록 열 이름
# 사업자번호, 법인명, 대표자, 업태, 종목, 사업장주소, 공급가액, 세액 사용
erpDic = {'사업자번호':0,'법인명':1,'대표자':2,'업태':3,'종목':4,'사업장 주소':5,'공급가액':6,'세액':7}
erpHash = dict() #열 이름을 키값으로 갖는 셀 위치
erpName = []
for c in range (0,erpWS.max_column):
erpHash[erpWS[2][c].value] = erpWS[2][c].coordinate.strip('0123456789')
print(erpWS[2][c].value,erpHash[erpWS[2][c].value])
erpVal = []
for i in range (3,erpWS.max_row+1):
temp = []
if erpWS[erpHash['사업자번호']+str(i)].value!=None and erpWS[erpHash['수금액']+str(i)].value!=None: #사업자명이나 수금액이 없다면 저장하지 않음
for j in erpDic:
if j=='대표자': #대표자 이름 전처리
temp.append(erpWS[erpHash[j]+str(i)].value.strip(' '))
else:
temp.append(erpWS[erpHash[j]+str(i)].value)
if temp[0] in emailAddress.keys(): #저장된 이메일 주소가 없을 경우 None
temp.append(emailAddress[temp[0]])
else:
temp.append(None)
erpVal.append(temp)
print(temp)
# 전자세금계산서 저장을 위한 이차원 배열
rowVal = []
dt = datetime.datetime.now();
for i in range (len(erpVal)):
temp = []
for j in range (taxWS.max_column):
if j==0:
temp.append('01')
elif j==1:
temp.append(dt.strftime("%Y%m%d"))
elif j==2:
temp.append(erpVal[i][erpDic['사업자번호']])
elif j==4:
temp.append(erpVal[i][erpDic['법인명']])
elif j==5:
temp.append(erpVal[i][erpDic['대표자']])
elif j==6:
temp.append(erpVal[i][erpDic['사업장 주소']])
elif j==7:
temp.append(erpVal[i][erpDic['업태']])
elif j==8:
temp.append(erpVal[i][erpDic['종목']])
elif j==9:
temp.append(erpVal[i][8]) #이메일
elif j==11:
temp.append(erpVal[i][erpDic['공급가액']])
elif j==12:
temp.append(erpVal[i][erpDic['세액']])
elif j==14:
temp.append(dt.strftime("%d"))
elif j==15:
temp.append(dt.strftime("%m")+'월 CCTV용역료')
elif j==19:
temp.append(erpVal[i][erpDic['공급가액']])
elif j==20:
temp.append(erpVal[i][erpDic['세액']])
elif j==50:
temp.append('01') #영수01 청구02
else:
temp.append('')
rowVal.append(temp)
print(temp)
for i in range (len(rowVal)):
for j in range (taxWS.max_column):
taxWS.cell(i+7,j+1,rowVal[i][j])
print(rowVal[i][j])
taxWB.save('data/test.xlsx')
erpWB.close()
emailWB.close()
taxWB.close()
주피터 노트북으로 실행
In [1]:
from IPython.core.display import display, HTML
display(HTML("<style>.container {width:90% !important;}</style>"))
In [2]:
import openpyxl
import os
import datetime
In [3]:
erpWB = openpyxl.load_workbook('data/erp.xlsx')
emailWB = openpyxl.load_workbook('data/email.xlsx')
taxWB = openpyxl.load_workbook('data/origin.xlsx')
In [4]:
erpWS = erpWB[erpWB.sheetnames[0]]
emailWS = emailWB.active
taxWS = taxWB[taxWB.sheetnames[0]]
In [5]:
emailWS[8][0].value
In [6]:
# 이메일 사업자 번호를 키로 해쉬테이블
emailAddress = dict()
for i in range(2,emailWS.max_row+1):
emailAddress[emailWS[i][0].value] = emailWS[i][1].value
print(emailWS[i][0].value,emailAddress[emailWS[i][0].value])
In [7]:
# erp 수금 기록 열 이름
# 사업자번호, 법인명, 대표자, 업태, 종목, 사업장주소, 공급가액, 세액 사용
erpDic = {'사업자번호':0,'법인명':1,'대표자':2,'업태':3,'종목':4,'사업장 주소':5,'공급가액':6,'세액':7}
erpHash = dict() #열 이름을 키값으로 갖는 셀 위치
erpName = []
for c in range (0,erpWS.max_column):
erpHash[erpWS[2][c].value] = erpWS[2][c].coordinate.strip('0123456789')
print(erpWS[2][c].value,erpHash[erpWS[2][c].value])
In [8]:
erpVal = []
for i in range (3,erpWS.max_row+1):
temp = []
if erpWS[erpHash['사업자번호']+str(i)].value!=None and erpWS[erpHash['수금액']+str(i)].value!=None: #사업자명이나 수금액이 없다면 저장하지 않음
for j in erpDic:
if j=='대표자': #대표자 이름 전처리
temp.append(erpWS[erpHash[j]+str(i)].value.strip(' '))
else:
temp.append(erpWS[erpHash[j]+str(i)].value)
if temp[0] in emailAddress.keys(): #저장된 이메일 주소가 없을 경우 None
temp.append(emailAddress[temp[0]])
else:
temp.append(None)
erpVal.append(temp)
print(temp)
In [9]:
# 전자세금계산서 저장을 위한 이차원 배열
rowVal = []
dt = datetime.datetime.now();
for i in range (len(erpVal)):
temp = []
for j in range (taxWS.max_column):
if j==0:
temp.append('01')
elif j==1:
temp.append(dt.strftime("%Y%m%d"))
elif j==2:
temp.append(erpVal[i][erpDic['사업자번호']])
elif j==4:
temp.append(erpVal[i][erpDic['법인명']])
elif j==5:
temp.append(erpVal[i][erpDic['대표자']])
elif j==6:
temp.append(erpVal[i][erpDic['사업장 주소']])
elif j==7:
temp.append(erpVal[i][erpDic['업태']])
elif j==8:
temp.append(erpVal[i][erpDic['종목']])
elif j==9:
temp.append(erpVal[i][8]) #이메일
elif j==11:
temp.append(erpVal[i][erpDic['공급가액']])
elif j==12:
temp.append(erpVal[i][erpDic['세액']])
elif j==14:
temp.append(dt.strftime("%d"))
elif j==15:
temp.append(dt.strftime("%m")+'월 CCTV용역료')
elif j==19:
temp.append(erpVal[i][erpDic['공급가액']])
elif j==20:
temp.append(erpVal[i][erpDic['세액']])
elif j==50:
temp.append('01') #영수01 청구02
else:
temp.append('')
rowVal.append(temp)
print(temp)
In [10]:
for i in range (len(rowVal)):
for j in range (taxWS.max_column):
taxWS.cell(i+7,j+1,rowVal[i][j])
print(rowVal[i][j])
In [11]:
taxWB.save('data/test.xlsx')
In [12]:
erpWB.close()
emailWB.close()
taxWB.close()
결과
프로그램 실행 결과는 다음과 같다.
test.xlsx
0.08MB
개선사항
- 최대한 확장성을 고려해 다른 회사에서도 사용할 수 있게 만들고 싶었으나, 머릿글 행(열 이름)의 처리 문제
- 전자세금계산서 발급을 위해서는 최대 1000건의 데이터만 입력해야 하는데 이를 위한 처리를 따로 해주어야 함
- 결과 파일의 배경 색상이 바뀌는 것의 원인을 확인하고 해결 해야함
'Programming > Side Project' 카테고리의 다른 글
| [PHP] 단순 기록 (0) | 2020.12.09 |
|---|---|
| [개발] 전자세금계산서 엑셀 양식 작성 프로그램: 웹사이트 배포 (0) | 2020.01.21 |
| [개발] Github를 이용한 무료 웹서버 호스팅: Github Pages (0) | 2019.12.03 |
| [사이드프로젝트] 사이드 프로젝트 진행하기 (0) | 2019.08.28 |
