[개념] Linear Regression & Cost Function: 선형 회귀와 비용 함수

2019. 10. 14. 17:41

Linear Regression이란

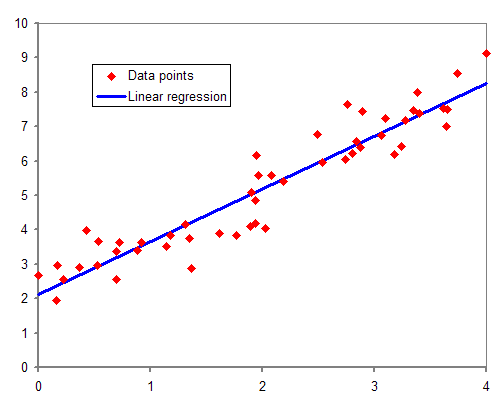
Linear Regression(선형 회귀)는 이전 머신러닝 개념 포스트에서 간단히 다루었던 지도 학습(supervised learning)의 한 종류이다. 선형 회귀는 학습 데이터(training data set)를 이용한 학습(training) 과정을 거쳐 데이터에 가장 잘 맞는 선형 모델의 매개변수(parameter)를 찾아 예측하는데 여기서 예측의 범위는 연속적인 범위를 갖는다. 다시 말해, 종속변수 y와 한 개 이상의 독립변수 x와의 선형 상관관계를 모델링하는 회귀분석 기법이다. 한 개의 독립 변수(또는 설명 변수)에 기반한 경우에는 단순 선형 회귀, 둘 이상의 독립 변수에 기반한 경우에는 다중 선형 회귀라고 한다. 실제로 많은 데이터들이 아래의 그래프와 같이 선형(linear)으로 분포하는 경향이 있기 때문에 선형 회귀를 통해 예측이 가능하다.

독립변수 1개와 종속변수 1개를 가진 선형 회귀의 예

선형 회귀는 선형 예측 함수를 통해 회귀식을 모델링하며, 알려지지 않은 매개변수는 주어진 데이터로부터 추정한다. 이렇게 만들어진 회귀식을 선형 모델이라고 한다.

선형 회귀의 대표적인 사용 사례는 다음과 같다.

값을 예측하는 것이 목적일 경우: 선형 모델을 통해 독립변수 x에 따른 종속변수 y를 예측하기 위해 사용할 수 있다.
종속변수 y와 독립변수 x 사이의 관계를 밝히는 경우: 선형 회귀 분석을 사용해 x와 y 사이의 관계를 정량화하기 위해 사용할 수 있다.

왜 Regression이라 하는가?

Regression을 영어 사전에서 찾아보면, 후퇴, 복귀, 쇠퇴, 회귀라고 나온다. 그중에서도 통계학 용어인 회귀는 국어사전에서 '한 바퀴 돌아서 본디의 상태나 자리로 돌아오는 것'이라고 한다. 이러한 용어는 영국의 유전학자 프란시스 골턴(Francis Galton)이 부모의 키와 아이들의 키의 상관관계를 연구하면서 키가 큰 사람의 아이가 부모보다 작은 경향이 있다는 사실을 연구하면서 소개하였다. 다시 말해, 키가 큰 부모보다 작은 아이의 키가 전체 키 평균으로 회귀한다는 것이다. 프란시스는 두 변수 사이의 상관관계를 분석하기 위해 사용한 방법을 회귀라고 이름 붙였으며 이후 칼 피어슨(Karl Pearson)은 아버지와 아들의 키를 조사한 결과를 바탕으로 함수 관계를 도출하여 회귀 분석 이론을 수학적으로 정립하였다.

선형 회귀식

선형 회귀는 주어진 데이터 집합에서 종속변수 y와 연관된 독립변수 x가 d개 존개하는 경우에 회귀식은 다음과 같이 나타낼 수 있다.

d개의 독립변수에 따른 선형회귀식은 다음과 같은 형태로 나타낼 수 있다.

여기서 y는 종속 변수 혹은 응답 변수라고 하며 출력값이라고 볼 수 있다. x는 독립 변수, 예측 변수, 입력 변수라고 하며 입력값이라고 볼 수

있다. ⍵는 매개변수, 회귀 계수라고 불리기도 하는 상수이다. b는 오차항, 노이즈로 이는 종속변수 y에 대한 모든 오차 요인을 포함한다.

가장 간단한 선형 회귀식은 독립변수 x가 1개인 1차 방정식 형태이다. 쉬운 설명을 위해 다음과 같은 형태의 회귀식을 사용하도록 하자.

여기서 H(x)는 입력값 x에 따른 출력 값 y를 예측하는 가설(Hypothesis)이며, ⍵와 b는 모델 파라미터를 의미한다. 이 ⍵, b파라미터를 조정하여 선형 함수를 표현하는 모델을 얻을 수 있다. 이 모델을 사용하기 위해서는 ⍵와 b를 정의해야 하며 이를 훈련 데이터에 가장 잘 맞는 값을 찾는 과정을 훈련시킨다(training)라고 한다. 그렇다면 어떻게 ⍵와 b를 정의해야 할까? ⍵와 b의 정의에 따라 1차 함수의 기울기와 절편이 달라지기 때문에 데이터의 산포도와 가장 적합한 함수가 될 수 있도록 ⍵와 b를 정의해야 한다.

선형 회귀에서는 일반적으로 선형 모델의 예측과 훈련 데이터 사이의 거리를 재는 비용 함수(Cost Function)를 사용한다.

비용 함수(Cost Function)

선형 회귀에서는 일반적으로 선형 모델의 예측과 훈련 데이터 사이의 거리를 재는 비용 함수(Cost Function)를 사용한다. 간단히 말해 각 점과 선 사이의 거리를 계산하며 가설(선형 모델의 예측)과 실제 데이터(훈련 데이터)가 얼마나 다른지를 평가하는 것이다. 이때, 단순히 하나의 데이터(single data)와 모델의 예측의 차이를 계산하는 것을 손실 함수(Loss Function)라고 하며 모든 데이터에 대한 차이를 모두 합하여 모델을 평가하는 것이 비용 함수이다.

선형 회귀식에서 ⍵와 b의 값에 따라 다양한 선형 회귀 모델을 만들 수 있다. 왼쪽의 그래프에서 볼 수 있듯이 세 가지의 선형 회귀 모델을 만들었다고 하자. 이 세 가지 모델 중에 가장 예측을 정확하게 하는 모델이 무엇인지 평가하기 위해서 비용 함수를 사용한다.

거리를 구하기 위해 위와 같은 식을 생각할 수 있으나 이 함수는 좋은 함수가 아니다. 단순하게 -y를 하기 때문에 y의 위치가 모델의 왼쪽과 오른쪽에 있을 때에 따라 같은 거리임에도 다르게 평가될 수 있기 때문이다. 따라서 비용 함수는 위의 함수를 제곱하여 사용한다. 다음 식에 m은 데이터의 개수를 의미하며 각 데이터에 대한 예측 결과를 실제 데이터와 비교하여 총 데이터에 대한 예측을 평가한다. 이 비용 함수의 결괏값이 적을수록 예측이 정확하다는 것을 의미한다. 가장 적은 비용을 갖는 ⍵와 b를 구하는 과정이 모델의 훈련 과정이다.