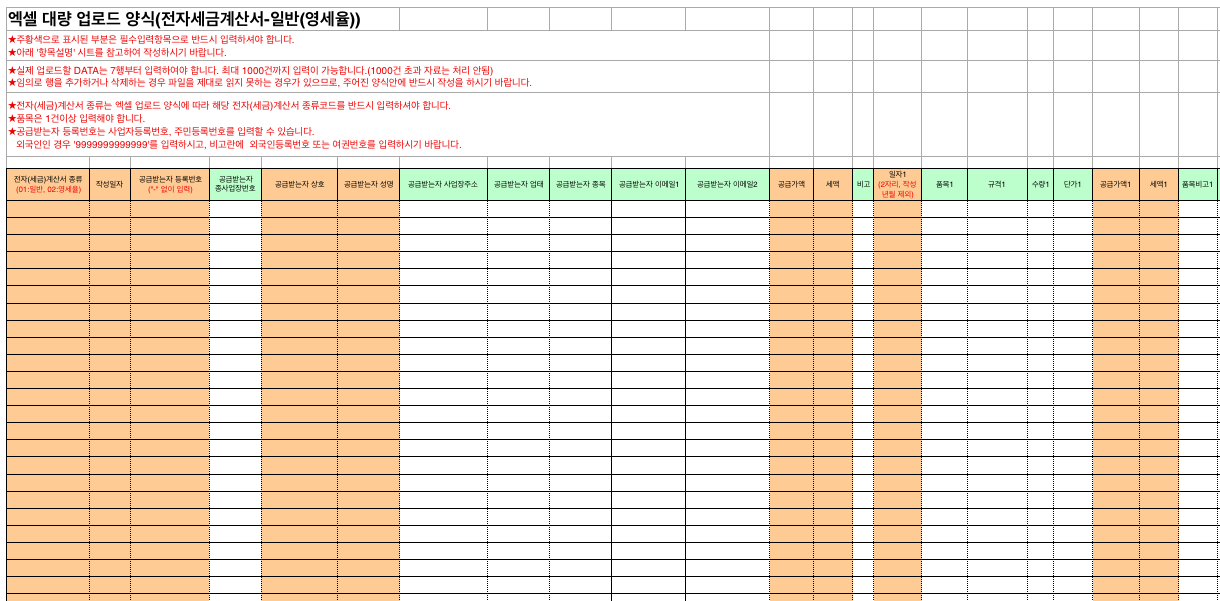
['01', '20191204', 1111111111, '', '자바', '제임스', '서울특별시 서초구 자바빌딩', '음식점업', '카페', 'java@java.com', '', 29000, 2900, '', '04', '12월 CCTV용역료', '', '', '', 29000, 2900, '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '01']
['01', '20191204', 2222222222, '', '씨', '벨연구소', '인천광역시 남구 씨대로 99', '도.소매', '컴퓨터판매', 'ccc@ccc.com', '', 35000, 3500, '', '04', '12월 CCTV용역료', '', '', '', 35000, 3500, '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '01']
['01', '20191204', 3333333333, '', '데이터', '디비', '서울특별시 강남구 데이터대로 베이스빌딩', '도.소매', '공장', 'data@base.com', '', 30000, 3000, '', '04', '12월 CCTV용역료', '', '', '', 30000, 3000, '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '01']
['01', '20191204', 4444444444, '', '파이썬', '귀도', '서울특별시 강남구 파이썬로 29', '도.소매', '꽃집', 'python@python.com', '', 60000, 6000, '', '04', '12월 CCTV용역료', '', '', '', 60000, 6000, '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '01']
['01', '20191204', 5555555555, '', '루비', '마츠모토', '경기도 시흥시 루비상가', '도.소매', '보석상', 'ruby@ruby.com', '', 20000, 2000, '', '04', '12월 CCTV용역료', '', '', '', 20000, 2000, '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '01']
['01', '20191204', 6666666666, '', '펄', '래리', '서울특별시 종로구 펄길', '음식점업', '횟집', 'perl@cperl.com', '', 35000, 3500, '', '04', '12월 CCTV용역료', '', '', '', 35000, 3500, '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '01']